原寸時の縦断線形
【 1.ことのはじまり 】
鋼上部工の原寸で橋の線形…というと、”線形座標図”という図面名が浮かびますが、
この図面の数値だけを見て橋の線形が頭に描ける人は多く無いと思います。
”線形座標図が無いと橋を作ることは出来ない!”と言われるほどに重要な図面なのですが、
線形座標図の表に示されている数値は、余程慣れていないと見づらいものです。
私が橋梁の原寸作業に携わって間無しの頃に教えられたのは、
”横桁(断面)は図面でも作れるけれど、主桁はうちの会社では作れない。”とか、
”顧客から仕事を貰うときは、脚とかアンカーフレームが望ましい。”ということでした。
そんなわけで当時の客先が支給してくれる資料の中に、線形座標図は有りませんでした。
実際、当時はまだ橋梁と言えば”超専門分野”のお仕事で、技術的な資料は”社外秘”扱い。
客先も外注業者に似合った仕事だけを出してくれていたし、それはそれで採算も合う時代でした。
初めて”線形座標図”が大切な図面だと知ったのは、橋梁の原寸に携わって2年後のこと。
ことの初めに”線形座標には数学系と測量系が有る。”と教えられたのを今でも覚えています。
概ね5、6桁の数値をタイプミス無く入力すれば、橋を作ることが出来る!
教えられるがままに作ったデータを使って、次々と出力される資料を見たときは、
”主桁も座標が有れば作れる!”という高揚感に包まれました。
以来私も”橋は線形座標で造るもの!”と当たり前のように言うようになったのですが、
さて皆さん、橋の線形座標ってどうやって作るのか知ってますか?
こう言うと、”地形を測量して、橋台の位置と高さを決めて…、座標を計算する。”
と答えるのが普通でしょうし、私も座標の細かな計算方法までは知りません。
”線形座標の作成は設計の所掌分野だし、原寸作業は座標に基いて作業するだけ。”
というのが一般的な考え方ですし、線形座標通りに原寸を行なうこと自体、容易では有りません。
でもこんな実情だけが、”主桁はうちの会社では作れない。”理由だったのでしょうか?
実際、システム原寸では格点の座標にキャンバーを載せれば橋を作れる印象も有ったのですが…。
それだけでは”ダメ!”と知ったことが、ことのはじめ。
格点間を補完する座標(一般的には中間V設置位置の座標)が重要なのです。
それをシステムが自動計算していたのだと気付いたのは、もう何年も前のことですが、
その仕組みまでは誰も教えてくれないのです。
以来こと有るごとにその仕組みについて調べ続けているわけですが、
いまだに”これが正解!”と断言出来る仕組みに辿り着けないことが悩ましいのです。
ある意味”自己満足”を得たいがための話にもなってしまうのですが、
一度こんな話でも、皆さまからご意見を頂けたらと思う次第です。^^;
【 2.何故ダメなのか? 】
ずっと以前の話ですが、何かの物件で主桁ウェブの修正作業が有りました。
(多分、中間V−stのピッチを調整したのかな…と思います。)
この作業を行うにあたってご存知の方は多いと思うのですが、
主桁ウェブをCADで表示すると、上縁(下縁)のラインは”折れ線”で構成されています。
これは一般的に格点と中間Vの位置をつなぐ”折れ線”なので、
中間Vの罫書きだけを移動すると”折れ点”の無い箇所にV−stを配置することになります。
元々縦断曲線を直線で近似する場合の”許容サグ量”は1ミリとか2ミリなので、
今なら迷わずにV−stのピッチだけを修正すると思うのですが…。
当時は”V−st位置には折れ点が必要!”だと思っていたようです。
”ウェブの上下縁に曲線を描いて、V−st移動位置の折れ点を求めれば良いのでは!”
私は金型製作でCADの手ほどきを受けていたので、
”主桁ウェブ上下縁のライン=スプライン(曲線)”というのが第一感。
”全然簡単じゃないか!”と思ったことが有ります。
まずその時点で”ダメ出し!”を受けたのですが、その時に言われたのが、
”スプラインは3次曲線では無い。”だったと思います。
今から思えば少し変な話なのですが(4点で作成するスプラインは3次曲線です)、
確かに一枚のウェブ上でブロック端>格点>格点>ブロック端の4点をつないだスプラインは、
微妙に中間V−st位置の折れ点とは一致しません。
何故?と言えば今では笑い話になりますが、当時はそんな問題でつまずいてばかり。
”格点を通る3点円弧で近似してくれたらいい。”
業を煮やした客先に教えられて実際にやってみても、まだ”ピッタリ!”とは重なりません。
しかしそれでも不思議なことに、スプラインで近似するよりは少し”マシ”でした。
こんなので良いのかなぁ…と思いつつも”格点間は3点円弧で近似。”を覚えました。
それにしても、何故スプラインではダメで3点円弧の方がマシなのか?
私はこの疑問を抱えたままで何年も、”皆が怖がる主桁ウェブのCL修正!”とか、
行なっていたわけですが、いつの頃からか、
”主桁の外形(上下縁の線形)を手修正するくらいなら、再計算を行なった方が楽。”
なくらいにシステムの性能がアップしてしまいました。
確かに主桁ウェブの外形を手修正するのは、”怖い”話なので助かっているのですが…。
仕組みを知らずにシステムの計算結果だけを信じるのも怖い話です。^^;
【 3.何故いまさら縦断曲線なのか? 】
人には色々と転機が有るものですが、私にとって大きな転機は”独立”でした。
それまで会社で行なっていた原寸作業を自宅で行える。
勿論そのためにはパソコンやらプリンターやら買い揃えなければなりませんが、
当初から感じていたのが、”仕事が無いときはどうしよう…。”という懸念です。
”仕事が無いときは、仕事を効率化するソフトでも作ろう!”
そう考えて購入した”Visual Basic”をいう開発ソフト。
”アイドル対策用”の仕事なので、飯の種には成らないのですが、
積み重ねているうちに、結構役立つようになりました。
これは線形座標が簡単にエクセルへ取り込めることを知った頃からだと思います。
エクセルの表で座標を扱えば、色々な資料を簡単に作成出来ると思ったのです。
(実際、縦断勾配や横断勾配は簡易計算出来ますし、結構複雑な計算も出来ます。)
”エクセルでここまで出来るのなら、Visual Basicならもっと出来る!”
そんなことまで思ったのが運の付き(苦悩の始まりかな)、
”何故スプラインではダメなのか?”を、検証してみようと思ったのです。
以来、3年余り(もうすぐ4年)いろんなことを試してみました。
勿論”アイドル対策”なので、時々思い出したようにプログラミング…なのですが、
まずはネットでの情報収集から始まって、数学のアルゴリズム入門書を購入したり、
サンプル資料を集めたり、知り合いの方々から色々なお話を伺ったり…。
そうこうする内に気付いたのは、
”この種の技術に関しては、情報や資料がとても少ないこと。”と、
”自分の聞き方が悪いのか、人によって返ってくる答えが微妙に違う。”ことでした。
いずれにしても数学の公式を使って計算しているのは間違い無いはずだから…。
と調べている内に見つけたのが、”ラグランジュ補間”の公式。
格点の座標値から格点間の補間値を求められる公式なので飛びつきました。
これだってプログラミングするのは容易では無かったのですが、
果たして結果は…手元に有るサンプルの数値とは似ても似付かぬ計算結果ばかり。
何故だろう?って考えても分りそうには無いので、他の方法で再挑戦!
しかし、2次関数、放物線、双曲線、3次関数…。
どの方法で計算してもサンプル通りの計算結果は再現出来なかったのです。
元々が計算の仕組みを調べることを目的としたプログラムなので、
そんなに複雑になるとは思っていたのですが、2次関数や3次関数が出てくると、
”連立方程式”を解くためだけに、新たなアルゴリズムが必要になったり…。
ここまで複雑になると、使っている公式が悪いのか、プログラミングが悪いのか、
分らないことに分らないことが重なって、一時期、挫折していました。
【 4.解決への糸口 】
元々がそんなに強い意志を持って!という話でも無かったので、
深刻に考え込んでいたわけでも無いのですが、心の奥底に残るのは”悔しい”想い。
忘れてしまいたい…とも思うのに、何故か本屋では”専門書”のコーナーへ足が向きます。
そうこうする内、何故か手にした”曲線表”という本。
それをパラパラめくるうちに、巻末近くの”縦断曲線”の図に目が止りました。
実は以前、ある人から”線形計算はこうやって定規をあてるようにして計算するのです。”
両手に持った割り箸で三角形を作りながら教えられたことが有ったのです。
その時はお酒の席での話だったので、まったく理解出来て居なかったのですが、
”縦断曲線の始端・終端の勾配”が、その時の割り箸に見えたのです。
早速ネットで”縦断曲線 縦距”を検索してみると…なんと、デザインデータブック!
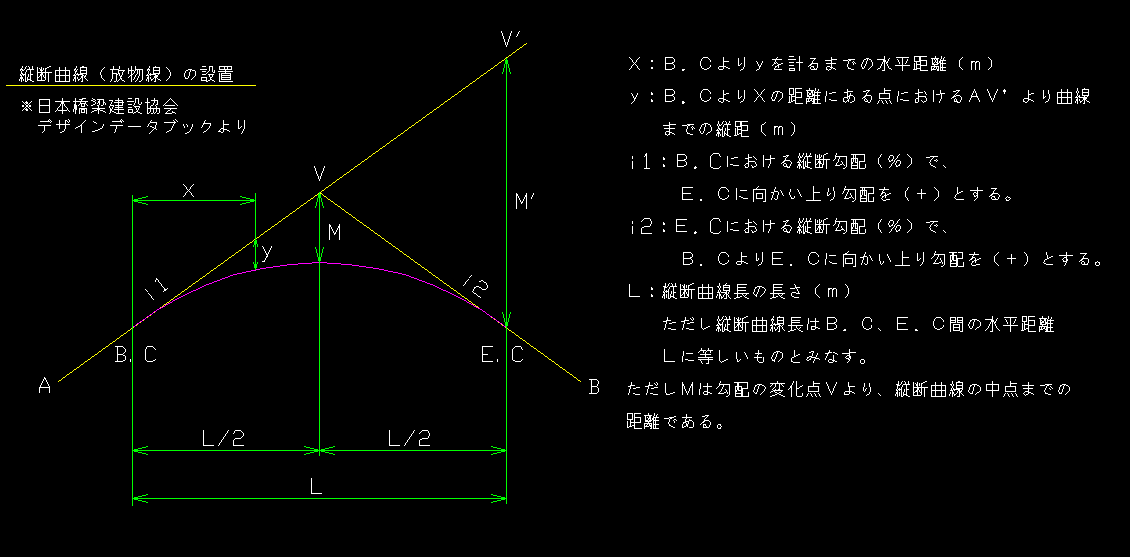
”えっ!何度も見たのに、今まで何で気付かなかったのだろう!”
兎にも角にも、y=((i1−i2)/200L)*X^2をプログラミング。
この公式を解くには、やはり2次関数を解かなければならないのですが、
今度は以前作成した”ガウス公式”のルーチンも有りました。
結果は…やはり良く無かったのですが、それでも誤差が小さくなったような…。
そう言えば、”y=”の式の上に有る”M=((i1−i2)/800)*L”は何だろう?
ということで修正したプログラムで計算した値を見てビックリ!
格点間の1/2位置だけは、小数点以下の数値までサンプルと一致したのです。
ここまで分れば、”何故スプラインではダメだったのか?”とか、
”何故、3点円弧の方が誤差が少なかったのか?”も、少し分ったような気がします。
実のところ、この”M=”の公式は、自動車が制限速度で走行した際に、
”乗り心地の良さを覚える縦断緩和曲線”を求める公式のようです。
元々は支点間や測点間の格点で勾配変化を緩和する座標を計算する公式のようなので、
格点間という5M程度の区間にまで適用するのが適切なのか?までは分りません。
実際のところ、こと”橋梁”関連でこの公式を探すのは難しいのですが、
土木(道路)関連のHPでは頻繁に出てくる公式です。
またこれもつい最近になって分かったのですが、
橋梁の原寸用線形の計算で使用されているプログラムが、
すべてこの公式を使っているのかどうかは分らないようなのです。
たまたま手にしたサンプルが”M=”を使っていたからピッタリ一致したのでしょうが、
4点を通る3次曲線だけでも計算出来るし、そんなに誤差も大きくないのです。
他の線形システムは他の考え方で計算していても不思議では無い。
そのことが尋ねた人によって答え方が微妙に異なった理由…なのかも知れません。
冷静に橋梁製作を考えると”格点のレベルは絶対に守ること(座標通りに作ること)”
という大前提が有る反面、”格点間の線形はこうする!”という規則は聞きません。
”3次曲線を用いて緩和計算をしています。”という証明さえ出来れば充分なのかも知れません。
だとしたら、格点間をスプラインで求めても良かったのでは?
そうです!格点のレベルを厳守して、スムーズなスプラインを作画出来るのなら良いはずです。
(但し、ウェブ1枚単位ではなく、全体図での作業になるはずです。)
もっとも”スムーズな曲線で作りました。”と言うだけでは、誰も納得しないと思います。
そんなに難しい説明をするくらいなら”3点円弧”の方が説明し易いことは自明です。
(こと格点間に限れば3点円弧の方が”円曲線”に近いと思いますし…。)
【 5.今後の課題 】
実はここまでして作成したプログラムですが、まだ課題が残っています。
確かに格点間の1/2点の座標はサンプル通り計算出来たのですが、
通常、格点間のV−stは3本くらい有るものです。
この1/4点座標を”y=”の公式や他の公式で計算すると、やはり誤差が大きいのです。
それを解決するために、格点と格点間の1/2点の座標を使って1/2点の勾配を計算し、
再度”M=”の公式で計算するのですが…。
多分勾配計算の問題だと思うのですが、左右1/4点でのレベルが±0.1ずつずれるのです。
(たかが0.1ミリ…と言うのなら、3次曲線だけで計算しても1ミリ以内の誤差なので…。)
何故か格点間の1/2点での接線勾配が正確に計算出来ていないようなのです。
原因が1/2点座標の誤差に有るのか、それとも勾配計算の考え方に有るのか?
誤差は小数1位まで無いし、勾配計算は3次曲線で計算しているのですが、
3次曲線の計算にどの座標を使用するのか?とか、どの値を平均するのか?など、
作ってみないと分らないような壁に直面しています。
皆さんからアドバイスを頂けたらありがたいのですが…。^^;
ちなみに格点間座標の問題を解決するためだけに作ったプログラムなので、
平面線形(クロソイド)や縦断折れ(KL)やキャンバーとかは、全然解決していません。
(サンプルデータも簡単な仕様なので、テストだって不充分。)
アイドル対策での”実験?”なので到底商用に使えるような代物では無いけれど、
目標は”弊社でも自前で主桁の原寸線形くらいは計算したい!”ことです。
私のような個人が線形計算のツールを持つことは、ある意味”永遠の夢”なので…。
ある意味”くだらない”話題にお付き合い頂きありがとうございました。^^;
原寸の線形計算…と言うと、案外、他人には理解して頂けない世界です。
実際、原寸検査では格点の座標は重要ですが、V−stのレベルは話題にもなりません。
だから…という話でも無いのでしょうが、今、汎用の線形計算システムは、
一貫システムの影に隠れて、忘れ去られようとしています。
(昔の汎用システムの方が小回りは効いたのですが…とか、聞くこともあります。)
一貫システムは保守やメンテナンスでバージョンアップされていきますが、
長いことお世話になった汎用システムは、機器の進歩に取り残されて、かわいそう…。
良いものは残したいし将来へも引き継ぎたいものですね。
私は最新の一貫システムも汎用システムの積み重ねの上に成り立っていると思うのです。
その積み重ねを知らずに成果だけを求めることには違和感を覚えます。
温故知新。
ご賛同頂けましたら幸いです!^^;
【 参考:格点間座標の計算方法 】
参考までに私が考えた計算方法を説明しておきます。
この考え方でも悪くは無いはずなのですが、なにしろ”原寸屋”の考えた方法です。
実際、何かがおかしいので精度誤差が出ているのも確かなので…。
ご意見を頂けましたら幸いです。^^;
図−1:計算で求めたい座標の確認
あくまでも求めたいのは”格点間の座標”です。
線形計算という言葉を使うと、”測点間の座標(格点)計算”を指すことも有るようですが、
与えられた格点の座標から、格点間の座標(中間V−st位置)のレベルを計算したい!
と言うのが目標です。
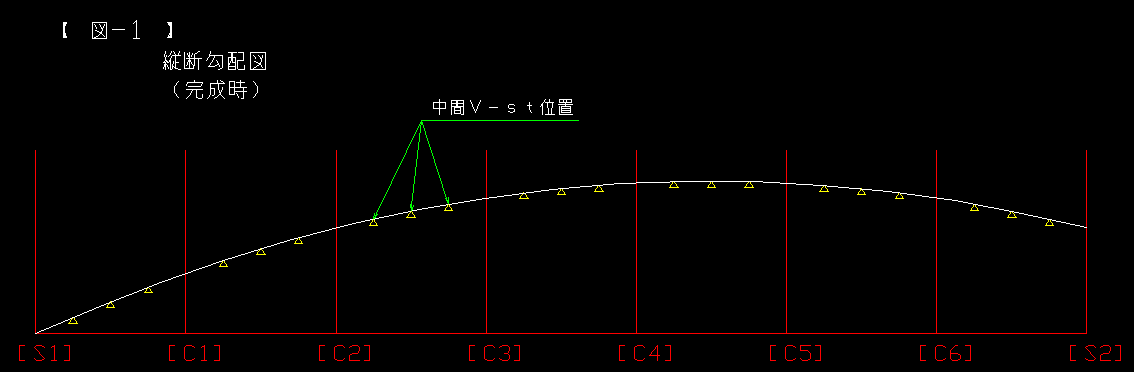
図−2:格点の勾配を計算する。
一般に言う”格点での縦断勾配”を計算する際の考え方です。
2次曲線を使用するべきか?3次曲線を使用するべきか?悩みました。
もしかしたらこの時点で計算した勾配に誤差が有るのかも知れません。
でもサンプルとした資料との勾配差は0.01%の桁まで発生していません。
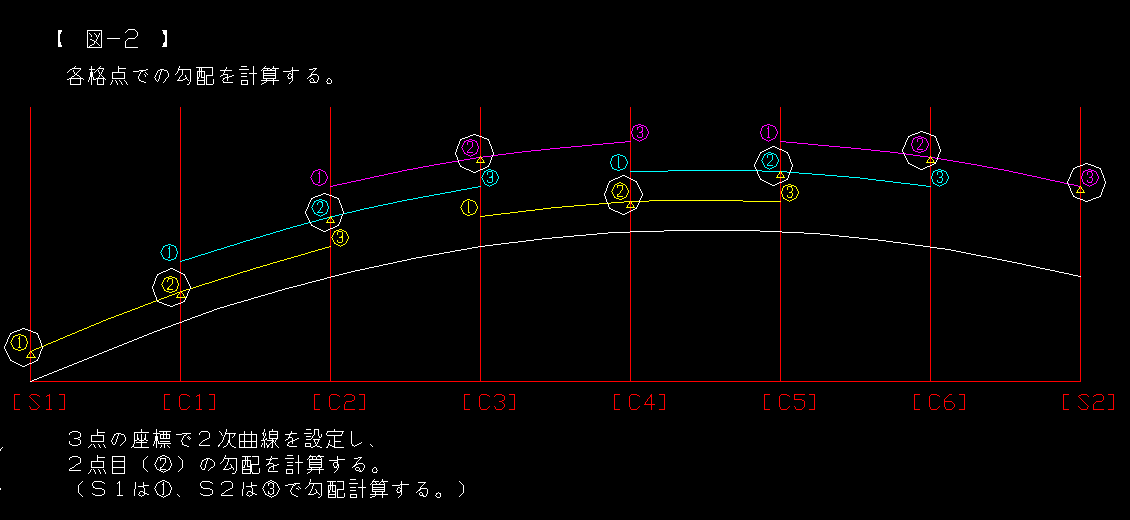
図−3:格点間中央での座標を計算する。
勿論、格点間の中央にV−stが有るとは限らないのですが、
最終的に曲線を折れ線で近似する際は、必ず”サグ量”の管理が必要になるはずです。
格点間を何分割すれば許容範囲に収まるのか?
…を考えたら、均等割りで徐々に精度を上げるのが正解なのかなぁ…と思いました。
”M=”の公式は接線から縦断曲線までの値を求める式なので、
B.C側の勾配とE.C側の勾配で各々レベルを計算して平均しています。
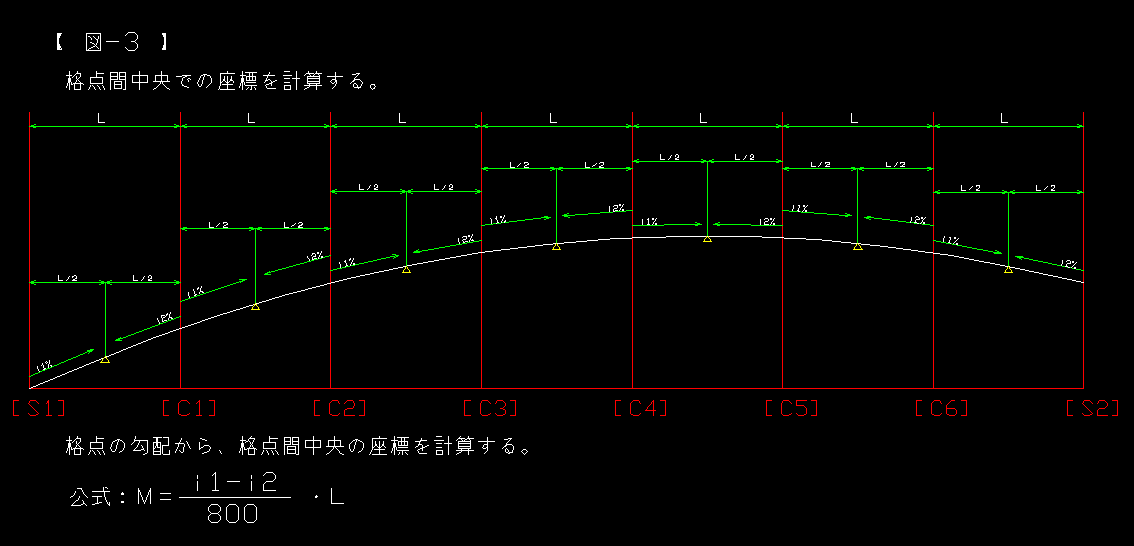
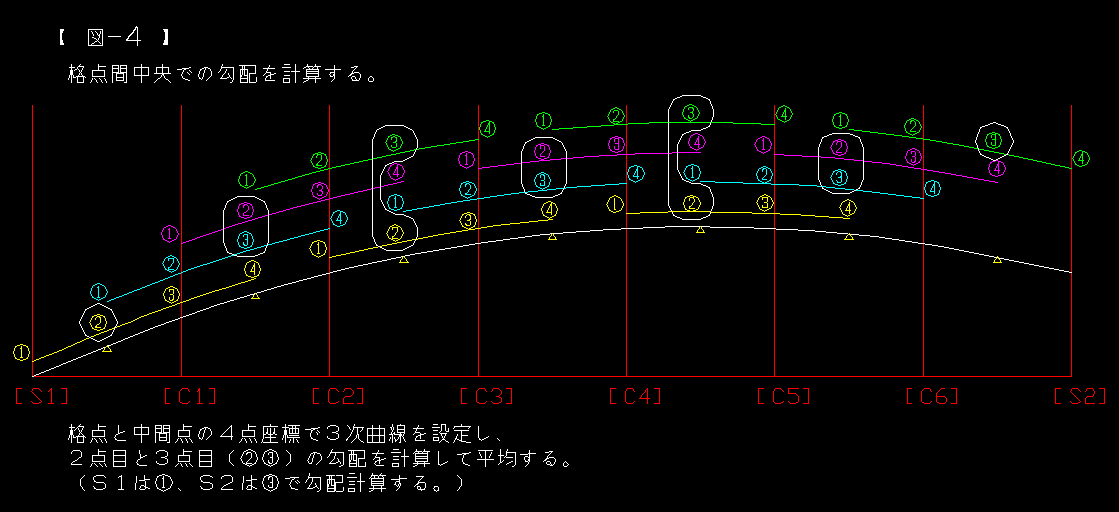
図−4:格点間中央での勾配を計算する。
格点の勾配を計算する際は2次曲線を使いましたが、中央の勾配は3次曲線で計算しました。
これは色々と試行錯誤していて気付いたのですが、
”M=”の公式で使用する縦断曲線は、両隣りの格点間の縦断曲線とは連続していない…?
元々各々の格点の勾配自体も異なった2次曲線で計算しているのだから、
中央の勾配を2次曲線で計算すると、格点で折れを作ることに成るのでは?
つまり格点間の縦断曲線を考える場合は、両隣りの縦断曲線とのつながりを考えないと
走行していて心地良い道路には成らない…ということです。
勿論、これが一番難しいことなので、これが精度誤差の原因かも知れません。
自分では2本の3次曲線で求めた値を平均することに無理が有るように思っています。
もしかすると3次曲線では無く、4次曲線で計算すれば解決するのかも知れません。
図−5:格点間1/4点での座標を計算する。
最初は”M=”の公式の傍に”y=”の公式があるので簡単だと思ったのですが…。
デザインデータブックの同じページの(1)放物線勾配の縦距も試したのですが、
結果的に両隣りの縦断曲線とのつながりを考えれば違うようです。
図の通り”M=”で計算する方法と、
中央部の勾配で使用した3次曲線で計算する方法が有ります。
両方試したのですが、3次曲線だと2つの曲線の平均になるので少し誤差が大きいようです。
”M=”だと現在手にしているサンプルとのレベル差は最大0.1ミリ。
誤差の発生状況に少し規則性が有るようなので、とても悩ましい問題です。

【最後に】4次曲線の可能性。
格点間中央の勾配を計算する際に、5点を使って4次曲線で計算する方法が有ります。
ガウスの公式を解くルーチンを作るときにそこまで考えて居なかったので、
3次用を4次用に改良するのが一苦労かなぁ…と思っています。
(勿論、他に方法が無ければ試してみるしか無いのですが…。)
造船では4次、5次の曲線で線形を計算するそうです。
2次、3次が解けたのだから、4次も5次も同じなのですが…。
橋梁の原寸線形って、本当にそうなのでしょうか?
2009/9/16記
メール:smo321@enjoy.ne.jp
入り口に戻る
メニューへ進む





