原寸入門(電卓編)
さて、皆さんの電卓を改めて見てみましょう。
電卓と名が付けば、”0〜1”の数字ボタン、”+、−、×、÷”の四則演算ボタンは有りそうです。
(勿論、”=”ボタンが無いと、計算結果を表示しなさい!という指示も出来ませんが…。)
今どき、携帯や時計にだって電卓機能は有るので、何ら珍しい代物では有りません。
では、皆さんの電卓を使用して”2の2乗”を計算してみましょう。
賢明な皆さんは、”2の2乗…2×2=の事じゃないか!”と気付かれるはずです。
(勿論、81の2乗ならば、81×81=で良い訳です。)
ところで、皆さんの電卓には”sin”とか”cos”とか”tan”と書かれたボタンが有りますか?
無ければ、価格は概ね1000円の電卓でしょうか?
でも、それ以外にも”X2”とか”√”とか”log”…訳の分らないボタンが有れば、少し高価ですね。
何事においてもそうだと思うのですが、物事に対する解決策は複数有るものです。
時と場合を考えて、ベストの選択が”2の2乗 = 2×2”ならば、”X2”の機能は不要です。
仮にも”関数電卓”と名が付けば、3000円程度の価格になってしまいますし…。
でも、あれれ^^;の原寸に対する抵抗感が和らいだのは、”tan”ボタンが使えるようになってからです。
このページのお話は、2000円の差額が生産設計(原寸)では、”必要不可欠な投資!”というお話です。
関数電卓って何?
先っきの、”2の2乗”を、もう一度考えてみましょう。
2乗というのは、”同じ数を賭け合わせる”のだから、当然、”2×2”です。
でも、掛け合わせる数字がとっても大きな数字だったらどうでしょう?
例えば、32768の2乗ならば、”32768×32768”と5桁の数字を2回押す訳です。
これが3乗、5乗ともなると…(5乗の計算なんてすることが無い!のも現実ですが…。)
そんな時、”X2”のボタンが有る電卓ならば、”32768 × X2 =”で良い訳です。
(3乗は、”32768 × X3 =”だし、5乗は、”32768 × Xy 5 =”ですね。)
いくら皆さんの指先が器用でも、同じ数字を何度も押せば、時間がかかるし間違うし…。
それを助けてくれるのが、”関数ボタン(X2とかtanとか…)”なのです。
以前は、1つの電卓にいくつの関数ボタンが付いているか?を自慢していた時代もありました。
今や、一つの電卓には、”たくさん”の関数・統計・単位変換機能が装備され、その全てを使いこなすのは不可能状態?
でも、”三角関数”の計算だけでも使いこなせたら、”関数電卓って便利”と思えるものです。
三角関数って何?
そう言えば高校の頃に習ったような…そう、sin、cos、tanです。
その言葉だけでジンマシンが…と思われる方も結構多いのですが…。
あのぉーー、私は日本の教育とか先生の資質云々を言うつもりは無いのですが…。
教科書の三角関数の1ページ目には、高い木の前に立った少年が、木の高さを計測する絵が有りました。
さて、現実には木の高さを三角関数で計算する必要は有るのでしょうか?
木の高さを測って何になるの?そんな架空の話のために、面倒な公式を覚えなきゃならないの?
私の知る限りそれは架空の話だと思うし、仮にあの絵が”ヘルメットを被った検査官”で
完成したビルの高さを検査している絵だったら…三角関数て、便利!と思ったかも…。
ちなみに、原寸をやっていて直面するのが、”投影長”と”実長”の違いです。
基本的に図面は投影長で描かれているので、それを実長に直すのが、生産設計(原寸)です。
その場合は、cos(コサイン)を使用すると便利なのですが…。
まあ、物事は順序が大切なので、まずはtan(タンジェント)をマスターしましょう。
それだけでも、”苦手意識”、が和らぐはずです。
TAN(タンジェント)って何?
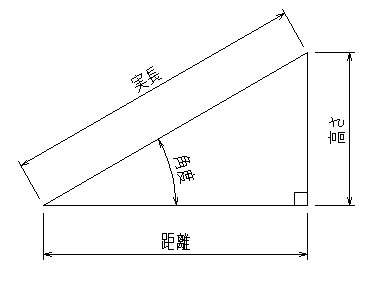
木の高さでも、ビルの高さでも良いのですが、”高さを求める関数(便利なボタン)”です。
ただし、これにはいくつかの条件が有って、
”高さを求めたい位置までの平面距離と角度”が必要です。
平面距離を計測するのは、案外、困難です。
例えばピサの斜塔だと、建物の根元までの距離は、テッペン位置までの平面距離では無いからです。
tanは、”距離と高さの成す角度が90°”っていう約束が有ってこそ、成り立つ関数なのです。
(しつこいけど、自然に生えている木だって微妙に傾いていると思う。)
”距離と高さの成す角度が90°”っていうことは、一般には”建物が真直ぐ建っている”という意味なのです。
角度の計測も、案外難しいです。
確かに、”水準器”を使えば、自分の目の位置から木のテッペンまでの角度が測れます。
木の高さを計るのだから、自分の目の高さと木の根元の差を調整するのは当然として…。
普通、大きな木の生えている場所は野山です。
木の根元と自分の足元が同じ高さ(標高)で無かったら…。
計測した角度を、そのままtan計算には使えません。
”距離と高さの成す角度が90°”っていうことは、一般には”地面が真平ら”という意味なのです。
前置きが長くなったけど、教科書に出ていたあの木は、まっ平らな地面に真直ぐ立っていた木なのです。
そう考えれば、直角(矩形)の多い”鋼構造物の原寸”には、利用出来そうです。
TAN計算
単純に、”
距離 × tan 角度
”と覚えて下さい。
(掛け算なので、”tan 角度 × 距離”でも良い。)
ちなみに角度30°の直角三角形の三辺の長さは、1:2:√3の関係が有りますよね。
だまされたと思って、”
√ 3 × tan 30 =
”と電卓のボタンを押してみましょう。
答えは”1”って表示されたでしょうか?
だから何なの?って思うのが普通だと思うし、思わない人はアクビが出る頃でしょうか?
ここで大切な事は、”1”って表示出来た瞬間、皆さんが、”
関数電卓を使った!
”という事なのです。
多分皆さんは、学生時代に好きでもない数学の教科書で、
tanθ = 高さ ÷ 底辺
という三角関数の公式を見た事が有ると思うのです。
(sinθ = 斜辺 ÷ 高さ 、cosθ = 底辺 ÷ 斜辺 でしたっけ?)
そう、あの公式を使って電卓で計算をしたのです!!
数学での約束、右辺と左辺(なつかしい?)の入れ替えを思い出して貰えれれば、
tanθ = 高さ ÷ 底辺 は、
tanθ × 底辺 = 高さ でも良いはずだから、
高さ = 底辺 × tanθ
にしても良いですよね。
それって、底辺は距離(√ 3)だし、tanθはtan 30のことなのです。
(ちなみに、斜辺は”実長”と言えば分かり易い?)
そうなのです。
関数電卓って、学生時代に習った”公式”を計算出来る”
便利な電卓
”だったのです。
この場合、注意を要するのは、距離と高さが90°の関係になっているのかどうか?だけです。
(なってなければ、なるように調整の計算が必要…ベテランはワザと難しそうにやっています。)
橋梁では、距離100で高さがいくら…という表記を多用します。
これは、工場で分度器が使用出来ない(差し金で角度を管理する)ので、使われる手法です。
tanが分ると、実際に工場で製作に携わっている人達の話が分るようになります。
その糸口が、距離と角度とtanボタンならば、重宝ですよね?
COS計算
cosボタンは、斜辺の長さ(実長)を計算する場合に、重宝しています。
(コサインは割り算と組合せて使用するので、ボタンを押す順番を間違うと、まずい!ですが…。)
単に実長を知りたいだけならば、”
√(X2 × Y2)
”でも計算出来ます。
(有名な”3平方の公式?”でしたっけ?)
だけど、角度が分かるのなら(逆tan…アーク・タンジェントで求められるなら)cosが便利なのです。
何故って、tanで使用する角度とcosで使用する角度は同じ角度…sinだけは違うけど…なのです。
よく有るのは、図面に距離と高さが指示されていて、実長を求めるという作業。
そんな時、”
高さ ÷ 距離 = Shift tan = 距離 ÷ cos Ans
”で実長計算が出来ます。
(Shiftボタンを押してからtanボタンを押すと、逆tan計算が出来ます。
またAnsボタンは、逆tanで求めた値を、電卓のメモリから呼び出すボタンとして使用します。)
先の直角三角形を例にすると、”
1 ÷ √ 3 = Shift tan =
”までで、角度の”30”が表示されます。
続けて、”
√ 3 ÷ cos Ans
”で、実長の”2”が表示されましたよね!
(最初から角度が分っていれば、”
√ 3 ÷ cos 30
”だけで、”2”と表示される訳です。)
ちなみに、他にも簡単な計算方法は有ります。
”POL(” ボタンを押した後に、 ”距離 , 高さ )” でも実長は計算出来ます。
”
POL( √ 3 , 1 )
” の順にボタンを押すと”2”と表示されるはずです。
(POLは、”座標変換”の関数です。)
勿論、”
√ 3 X2 + 1 X2 = √ =
”でも結果は同じです。
好きな方法を使えば良い…取り敢えず電卓に慣れれば、いずれcosが一番便利と実感出来ます。
繰り返すけど、cosは割り算との組み合わせなので、順番が大切。
”
距離 ÷ cos 角度 =
”
距離が先!
って覚えましょう。
ここまで出来れば先輩達も、グッと真剣な表情で、あなたの話を聞いてくれます。
同じ三角関数でも、あれれ^^;は、”sin”を滅多に使用しません。^^;
多分、図面を描く人が、X軸とY軸に沿って寸法を表記するからでしょうね。
(設計担当者には、斜辺の長さを表記するような余裕など無いものです。
でも案外、”角度”は、図面に表記されているものです。)
図面は投影長、原寸は実長!図面は原寸用に画かれている?といった甘い考えは止めましょう。
誰が見ても簡単に作業の出来る図面ならば、最初から原寸作業者など不要なのですから…。
皆様の健闘をお祈り致します。
初心に戻る
メニューに戻る
